
Research Statement
PDF version
“Intellectual growth should commence at birth and cease only at death.” [Albert Einstein]
Albert Einstein once said, “Intellectual growth should commence at birth and cease only at death.”[1] As an academic, the importance of keeping current on the modern mathematical developments is self-evident. Often times, the best researchers are the best teachers. Research and publications also promotes the good name of the College and benefits the society as a whole. This statement will serve to demonstrate how I have demonstrated these important qualities through research in the past and will serve as a road map for where I would like to take my research in the future.
Why would someone put a random $6 \times 6$ array on their CV (see Figure 1)? This particular array is special to me in that it is one of 1,393,920 latin squares where in addition to the rows and columns, every $2 \times 3$ region and every $3 \times 2$ region have symbols $1$ through $6$ exactly once.
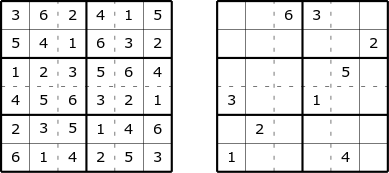
In addition to enumerative problems, colleagues of mine as well as undergraduate students have latched on to existence problems regarding these designs as well as generalizations of these designs. To date, we know that such designs, called Sudoku Pair Latin Squares, exist when one of the factors is less than or equal to $3;$ so, the smallest unknown design is order $28,$ where every row, column, $4 \times 7$ and $7 \times 4$ region have numbers $1$ through $28$ exactly once. On a similar note, I co-mentored a group at the Moravian REU last summer that was investigating how large the positive difference between adjacent symbols could be in such a design. To entice students and other mathematicians to do research in this field, I have been occupying my time by making a puzzle book out of a subset of these puzzles such as the one in Figure 1. Such designs can be used to conduct agricultural experiment and help reduce nuisance variables.
But I know, puzzles aren’t for everyone. They’re an easy sell to a lot of students and mathematicians, but not for all. In addition to latin squares, I am also interested in Structural Graph Theory. My primary interests in Graph Theory are graph coloring problems, graph domination problems, and graph decompositions.
Graph decompositions bridge the gap between Graph Theory and Design Theory. Two undergraduate students, a colleague of mine, and I have been trying to find necessary and sufficient conditions for the existence of a $K_3$-decomposition of Kneser Graphs (also known as triangle decompositions). This type of $2$-design has the emotionally satisfying property that every pair of elements appears in exactly one triple together. An example of such a decomposition is depicted in Figure 2. These designs can be used to conduct statistical analysis; however, I must confess that applications of such designs is not something I have studied. I am willing to delve into this subject if anyone is interested, however!
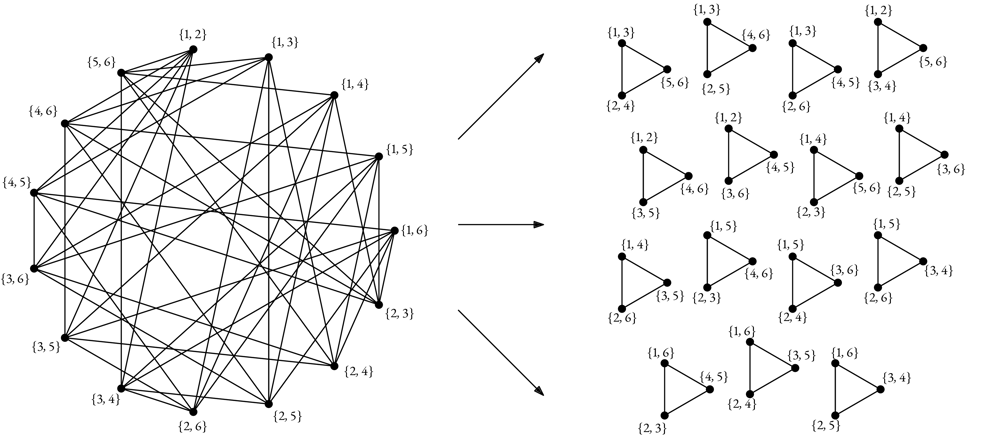
In addition, many aspects of the graph decomposition problem can be modified to ask different questions. We can modify the family of graphs that we are trying to decompose or we could modify the types of subgraphs that we are decomposing the family of graphs into. For example, in $2018,$ I worked with an REU group at Moravian researching decompositions of complete graphs into edge disjoint Halin subgraphs, which are essentially cycle graphs with a tree inside.
Transitioning out of the Design Theory realm into something more purely graph theoretic, I am also interested in graph domination. In graduate school, I worked with two of my colleagues to find the smallest DI-pathological graph with respect to both vertices and edges. Since then, a group of REU students from Muhlenberg and I have just gotten a paper published regarding the domination number of permutation graphs. While a graph is formally defined in terms of set theory, I feel that graph domination really relies on set theory more than any other subset of the field. This is one of the things that draws me to graph domination, and I know that some students and mathematicians are drawn to it for the same reason.
With respect to graph colorings, a colleague of mine and I co-mentored a group of REU students at Moravian the past two summers researching the strong connection number and the very strong connection number of graphs. While the name might not sound like it, these are really graph coloring problems. The problem aims to prove a Vizing type bound for a coloring so that between every pair of vertices, there exists a shortest path that is properly colored. A natural modification that we also studied was requiring that all of the shortest paths are properly colored. We are still working on this problem with the REU students, and I am confident that we will get a paper out of it in the near future.
While it might seem that this is off of the beaten path a bit, another area of interest for me is in covering systems. These systems of congruences aim to cover all of the integers with distinct modulus classes. An example of such a system is
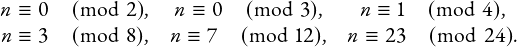
While this does not seem related to graph theory, the way we typically visualize this is by making a rooted tree to ensure that we are covering all of the integers exactly once. Along with a colleague, I have been able to successfully publish a paper which created an odd covering (all of the moduli are odd) of the integers using $5$ as a modulus three times, answering a question in the literature on the subject. Covering systems also have applications in number theory in finding special types of numbers like Sierpinski and Riesel numbers.
In conclusion, the reason that I gravitate to both Design Theory and Graph Theory is that the questions are typically easy to state, but difficult to prove. Most of the questions in these fields do not take a great deal of background to state; so, one can get to work on them rather quickly. Most of the topics, as you can see, have some sort of visual representation to them as well, which I also find alluring. As a visual learner, I appreciate when something has a figure to go along with it, and I think that a lot of students and people in general gravitate towards topics that have a visual representation. The goal of my research is to share my love of mathematics with as many people as possible.
References
- M. Jackson, D.D. Ignatavicius, and B. Case, Conversations in critical thinking and clinical judgment, Jones and Bartlett Publishers, 2005.